Zephyr: Direct Distillation of LM Alignment: Method

Table of Links

• Abstract and Introduction
• Related Work
• Method
• Experimental Details
• Results and Ablations
• Conclusions and Limitations , Acknowledgements and References
• Appendix

3 METHOD

The goal of this work is to align an open-source large-language model to the intent of the user. Throughout the work we assume access to a larger teacher model πT which can be queried by prompted generation. Our goal is be to produce a student model πθ and our approach follows similar stages as InstructGPT (Ouyang et al., 2022) as shown in Figure 2.

Distilled Supervised Fine-Tuning (dSFT) Starting with a raw LLM, we first need to train it to respond to user prompts. This step is traditionally done through supervised fine tuning (SFT) on a dataset of high-quality instructions and responses (Chung et al., 2022; Sanh et al., 2021). Given access to a teacher language models, we can instead have the model generate instructions and responses (Taori et al., 2023), and train the model directly on these. We refer to this as distilled SFT (dSFT).

Approaches to dSFT follow the self-instruct protocol (Wang et al., 2023). Let x 0 1 , . . . , x0 J be a set of seed prompts, constructed to represent a diverse set of topical domains. A dataset is constructed through iterative self-prompting where the teacher is used to both respond to an instruction and refine the instruction based on the response. For each x 0 , we first sample response y 0 ∼ πT(·|x 0 ), and then refine by sampling a new instruction (using a prompt for refinement), x 1 ∼ πT(·|x 0 , y0 ). The end point is a final dataset, C = {(x1, y1), . . . ,(xJ , yJ )}. Distillation is performed by SFT,

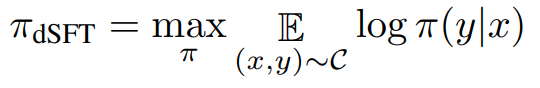
AI Feedback through Preferences (AIF) Human feedback (HF) can provide additional signal to align LLMs. Human feedback is typically given through preferences on the quality of LLM responses (Ouyang et al., 2022). For distillation, we instead use AI preferences from the teacher model on generated outputs from other models.

We follow the approach of UltraFeedback (Cui et al., 2023) which uses the teacher to provide preferences on model outputs. As with SFT, the system starts with a set of prompts x1, . . . , xJ . Each prompt x is fed to a collection of four models π1, . . . , π4, e.g. Claude, Falcon, Llama, etc, each of which yield a response y 1 ∼ π1(·|x), . . . , y4 ∼ π4(·|x). These responses are then fed to the teacher model, e.g. GPT-4, which gives a score for the response s 1 ∼ πT (·|x, y1 ), . . . , s4 ∼ πT (·|x, y4 ). After collecting the scores for a prompt x, we save the highest scoring response as yw and a random lower scoring prompt as yl . The final feedback dataset D consists of a set of these triples (x, yw, yl).

Distilled Direct Preference Optimization (dDPO) The goal of the final step is to refine the πdSFT by maximizing the likelihood of ranking the preferred yw over yl in a preference model. The preference model is determined by a reward function rθ(x, y) which utilizes the student language model πθ. Past work using AI feedback has primarily focused on using RL methods such as proximal policy optimization (PPO) to optimize θ with respect to this reward. These approaches optimize θ by first training the reward and then sampling from the current policy to compute updates.

Direct preference optimization (DPO) uses a simpler approach to directly optimize the preference model from the static data (Rafailov et al., 2023). The key observation is to derive the optimal reward function in terms of the optimal LLM policy π∗ and the original LLM policy πdSFT. Under an appropriate choice of preference model they show, for constant β and partition function Z that,

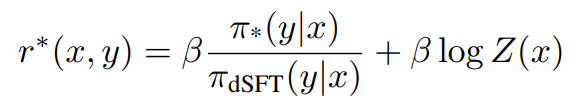
By plugging this function of the reward into the preference model, the authors show that the objective can be written as,

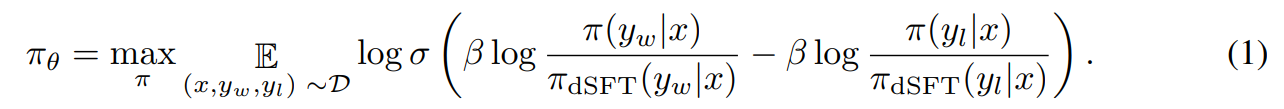
While this term looks complex, we note that it implies a simple training procedure. Starting with the dSFT version of the model, we iterate through each AIF triple (x, yw, yl).

1. Compute the probability for (x, yw) and (x, yl) from the dSFT model (forward-only).

2. Compute the probability for (x, yw) and (x, yl) from the dDPO model.

3. Compute Eq 1 and backpropagate to update. Repeat.